در برکه ای 7 قطعه سنگ وجود دارد که از چپ به راست با اعداد 1 تا 7 شماره گذاری شده اند.
قورباغه ای روی سنگ شماره یک نشسته است. فاصله سنگ ها به گونه ای است که اگر قورباغه روی سنگ i ام باشد می تواند حداکثر تا i سنگ جلوتر بپرد. به چند طریق ممکن است قورباغه، بدون برگشتن به سمت چپ، به سنگ شماره 7 برسد؟
الف) 10 ب) 11 ج) 12 د) 13
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
••••
جواب معمای المپیادی: عبور قورباغه از برکه
جواب گزینه ب 11 تا
روش سوم :
گزینه ی (ب) صحیح است.
بیایید از آخر مسئله را حل کنیم. فرض میکنیم که در حال حاضر روی سنگ i-اُم هستیم و تعداد روشهای مختلف برای رسیدن به سنگ ۷اُم را یادداشت می کنیم. ابتدا مسئله را برای سنگ ۷اُم حل می کنیم (۱ روش).
سپس برای سنگ ۶اُم و ...
در هر مرحله کافی است که برای سنگ iاُم، مجموع تعداد روشهای سنگهای 1 +i اُم تا 2iاُم را محاسبه کنیم. در نتیجه جواب مسئله اینگونه به دست می آید:
7: 1 → 6: 1 → 5: 2 → 4: 4 → 3: 7 → 2: 11 → 1: 11
روش دوم: استفاده از گراف های جهت دار و استفاده از ماتریس مجاورت آن است
در زیر نگاه کنید
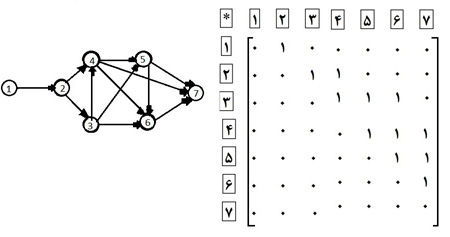
چون مسیر ها در واقع از 2 شروع می شود در کل 11 مسیر داریم . قسمت 1 به 2 در همه مسیر ها مشترک است
روش اول : استفاده از الگویابی منظم و رسم شکل است
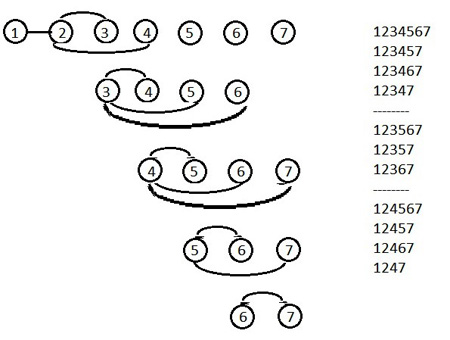
منبع:mathgroup.blogfa.com










